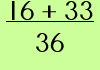Add Subtract Fractions

			$multiplyfractions$

			$dividefractions$

			$lowesttermsfractions$

	Adding and subtracting fractions are basically the same; the only difference is the operation (you add or you subtract!).There are two rules to remember when performing this basic skill and if you can remember these two rules, the rest is easy-peasy, lemon squeezey!

	In order to be able to add or subtract fractions, they MUST share a common denominator.

	Does this sound difficult? Naaahhh…so, let's try a method or two out and see how it works.


		Here is an addition problem where the two denominators are not the same. We are going to use the 'least common denominator' method to simplify.

You need to come up with a common denominator. So, find the LEAST common MULTIPLE (LCM) which is the same thing.

$fractmetho2a$

First, write down the denominators

$fractmetho2b$

and then draw this shape, kind of like the division 'box' but upside-down…

$fractmetho2c$

Begin to factor out common divisors (what factors do both of the numbers have in common?).

Use your divisibility rules to help you.

Start dividing (basically, you are dividing but upside-down!) until you can't find any common factors/divisors.

$fractmetho2d$

When there are no factors left (you have come down to all of the common factors), then multiply ALL of the numbers that are on the OUTSIDE of the 'box.'

*Notice that when you are multiplying the numbers, the shape made is an L!

This will give you the LCM (least common multiple). This becomes your new DENOMINATOR.

$fractmetho2g$

$fractmetho2f$

$fractmetho2e$

Now, criss-cross. This will tell you what you will be multiplying the numerators of each of your original fractions by.

Following the green arrow, you are going to multiply the 4 from 4/9 by 4.

Following the red arrow, you are going to multiply the 11 from the 11/12 by 3.

$fractmetho2h$

Perform your operation (in this case, addition).

If necessary or possible, reduce to lowest terms.

*In Algebra, you will probably leave your fraction as an improper fraction.

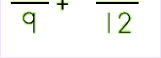Now, you know that you must have a common denominator before you can add or subtract fractions. So, another method is to find equivalent fractions and the Multiplicative Identity (also known as the 'Property of One') to help in simplifying your expressions.

Let's try this method when we want to subtract the following:

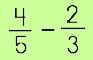					$fractions2$
			Here we have two fractions that have *different denominators*.

	The fastest way to do this is to MULTIPLY the two denominators. Under your original problem, draw a long division bar. Under the bar, write the two denominators and multiply them as shown.
			$fractions3$

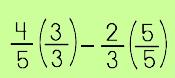					$fractions4$
			Using the Multiplicative Identity, you are going to change each fraction into an equivalent fraction. Note that on the left side, we are multiplying by 5/5. On the right side we are multiplying by 3/3. Both 5/5 and 3/3 are actually just the same as multiplying by one whole! We are simply re-naming our original fractions and giving them a 'new' name; sort of like when a girl gets married and takes on her husband's last name. The denominators, however, are simply being multiplied by themselves; just like in step #1.

	$fractions6$
Multiply 5 • 2 = 10 and 4 • 3 =12 so we can simply write 12 – 10 for our numerator as shown.		$fractions6$

	$fractions6$

Subtract the numerators. The denominator remains the same.

That's it! Easy-peasy!

Now, here's the deal: depending upon what is required (if it is written i the book's instructions OR what your TEACHER asks you to do!), you may be asked to change all improper fractions to mixed numbers. For MOST algebra problems, keep your answer as an improper fraction in LOWEST TERMS. That's it!


			Easy-peasy, lemon-squeezey! Download a practice page. Adding and Subtracting Fractions

$Rule #1: When adding/subtracting fractions,$