|
Dividing fractions is almost the same thing as multiplying fractions but with an added step (after all, we are DIVIDING fractions, right?). There are a number of ways to explain this particular concept so see which one works best for you.
|
|
 |
|
|
|
 |
|
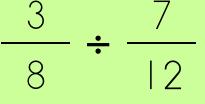
Let's see how we work our way through dividing with this particular fraction expression.
Following along…
|
|
|
|
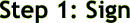 |
|
|
|
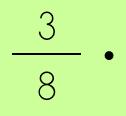 |
|
|
|
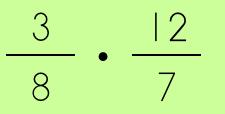
The first step is to change the sign. Begin re-writing the problem and instead of having the division symbol switch it to a multiplication sign. Don't be lazy! By re-writing the problem you will be able to see the numbers unfold…
|
|
|
|
|
 |
|
|
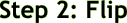 |
|
|
|
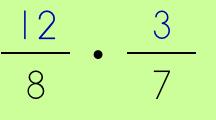
Now, you are going to FLIP the second fraction (take the reciprocal or the inverse). Write it.
|
|
|
|
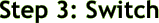 |
|
|
|
 |
|
|
|
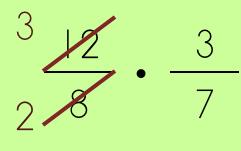
Next up? The switch! Yep, sounds odd but, just trust me. Switch the numerators.
*The Commutative Property of Multiplication allows you to do this, of course.
|
|
|
|
|
 |
|
|
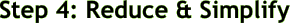 |
|
|
|
You can now reduce or simplify, if possible.
|
|
|
|
|
 |
|
|
|
|
|
|
Multiply the numerators. Then, multiply the denominators.
Voila! That's it!
(unless, of course, your teacher wants all improper fractions converted to mixed numbers)
|
|
|
|
 |
|
|
|
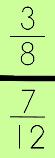 |
|
|
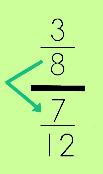
This method is a bit untraditional, BUT, I can guarantee that you will like it! Why? Well, for one, there are always math problems on those standardized tests that come in formats that are scary looking (for example, they look like this! EEK!).
But, when you break 'em down, you will see that they really aren't difficult at all! It is all PERCEPTION (how you LOOK at things).
|
|
|
|
|
 |
|
|
 |
|
|
|
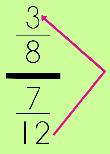
Most people eat the INSIDES of the Oreo cookie first, right? Look at the INSIDE numbers first. Multiply these and they become your 'new' denominator.
In this case, 8 • 7 = 56
*If you look carefully, you can see that the 8 is being brought down to multiply with the 7…
|
|
|
 |
|
|
|
|
|
 |
|
|
 |
|
|
|
Next, people eat the outsides of the Oreo cookie, right? So, what you do now is look at the OUTSIDE numbers.
Multiply these and they become your 'new' numerator. For us, this is 3 • 12 = 36
*If you look carefully, you can see that the 12 is being brought up to multipy with the 3…
|
|
|
 |
|
|
|
|
|
 |
|
|
|
|
|
|
Now, simply reduce your fraction like you usually would, in whatever method works best for you!
|
|
|
|
|
Are you ready for some practice? Download a practice page. Dividing Fractions
|
|