|
One of the hardest concepts in middle school math is learning about ratios and proportions. Why is this? As a teacher, I think it is because it all comes down to…drum roll, please! The F WORD! Yep, it's the ol' fractions thing, once again. IF you are comfortable with fractions, then ratios and proportions are really quite simple and the ONLY thing you have to remember is this: READ and write the information down IN ORDER.
Let's see what this looks like…beginning with vocabulary!
|
|
|
|
 |
|
|
|
Ratio…What is a ratio? A ratio is a comparison so understanding this particular vocabulary word is going to be KEY in figuring out proportions. Let's begin with ratios, then shall we?
There are three ways to write a ratio. The thing to remember with ratios is that ORDER is important.
- You can use a colon :
- You can write it as a fraction
- You can write it in words (the word 'to')
|
|
|
|
 |
|
|
Look at this group of butterflies. How many are blue? How many are red?
|
|
|
|
Let's make our comparisons now.
What is the ratio of blue butterflies to red butterflies?
(remember, ORDER is important)
There are three ways to write the ratio:
- with a colon
- 3 blue : 5 red
-
- as a fraction
- 3 blue
- 5 red
-
- in words
- 3 blue to 5 red
|
|
|
|
IF we didn't keep the order, then, look at what we'd have.
- 5 red : 3 blue
-
- which means something totally different!
|
|
|
|
 |
|
|
|
|
Middle school standardized tests ALWAYS have lots and lots of word problems dealing with proportions. Well, guess what! IF you can set up the problem correctly, then YOU can solve 'em easily! Yaaaa-hooo! All it takes is being able to READ the problem and finding the information and putting it into the right order.
Here's a typical word problem:
- Karla earns $36 for 3 hours of work. At that rate, how long would she have to work to earn $720?
|
|
|
|
So, let's see the steps in how we can solve this particular problem. Don't be shocked to find it really isn't that hard at all!
|
|
|
Step 1: Read the question. Find the numbers and labels of what you know. Underline them. From the problem we now have:
|
|
|
|
- $36 for 3 hours
|
|
|
|
- $36
- 3 hours
|
|
|
Take this information and re-write it as a ratio but in FRACTION form (remember, who is your BFF?)
|
|
|
|
|
Step 2: Find the numbers and labels of what you need to know. Underline them. We now have:
|
|
|
|
- x hours for $720
|
|
|
|
- $720
- x hours
|
|
|
Take this information and re-write it as a ratio but in FRACTION form
|
|
|
|
|
Step 3: Set up your problem as an EQUATION. Solve it. (How? Think…Did you come up with 'cross-multiply?' Yaaahoo!)
|
|
|
|
- $720
- x hours
|
|
|
- $36
- 3 hours
|
|
|
 |
|
|
|
|
|
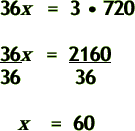 |
|
|
|
Step 4: Voila! Go back and put your solution back into the context of the question.
|
|
|
|
- 60 hours
|
|
|
 |
|
|
|
Try a few problems on your own.
- The geography map uses a scale of 1 inch equals 25 miles. How many miles are represented by 5 inches on this map.
- Farmer John harvested 14,000 pounds of oranges on 8-acres of his farm. If he has 30 acres of orange trees on his farm, approximately how many pounds of oranges could he harvest?
- The atmosphere normally exerts a pressure of approximately 15 pounds per square inch on surfaces at sea level. Approximately how much pressure does the atmosphere exert on a surface 30 square inches in area?
- In Honduras citizens use lempira for their monetary unit. In 2002 the conversion rate for U.S, money to Honduran money was about 6¢ to 1 lempira. What dollar amount would you get for 300 lempiras?
- Daniela's car gets an average of 28 miles per gallon of gas. She plans to drive 200 miles today and 220 miles tomorrow. How many gallons of gas should she expect to use for her trip?
|
|