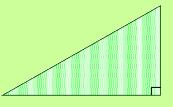
Now wasn't finding the Area for a parallelogram totally awesome? Well, you're in for a treat with the triangle!

Here we have a triangle with a base of 6 cm and a height (or altitude) of 4 cm.

OMG!! Do you see what I see? No, I'm NOT talking about the olive or the carrot sticks, silly. It's the TRIANGLE! When my mom would make me sandwiches then cut them, guess what! She would alwys (gasp!) cut them into triangles!

Hmmm…could this mean what I think it does?

Yes! A triangle is half of a parallelogram so its area formula is one-half of the parallelogram's Area formula.

It could also be thought of as:

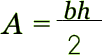This means that our original triangle could be viewed as one-half of a parallelogram (or because it is a right triangle, it could be one-half of a rectangle). So, let's compute its area.

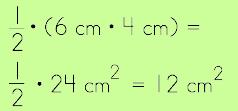So, whenever you are finding the Area of a triangle, maybe you should go and make yourself a sandwich.

Why? Because it will remind you to take HALF the area of a rectangle, of course!

Remember to look for the right angle symbol so that you can determine the base and height and don't end up using the wrong leg numbers!

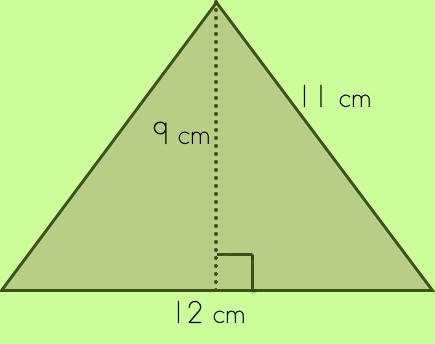Remember: Since the cm is also squared, the units will be 'square units.'

Try this one on your own.
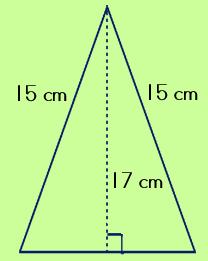