When you think about circles there are basically two formulae that, in middle school, you have to memorize. The problem is this: which formula goes with circumference and which one goes with area? Argh! If this is you, then don't sweat, the answer is easy-peasy, lemon-squeasy!

Did you do the finding π activity? If you did, then did you save your little strip of paper? That will help you tremendously. Yep, it sure will. Let's see just why I told you to keep that bit of scrap paper…

1. What do we call the distance across a circle, through the center?
2. What do we call the distance around a circle?
3. Approximately how many times were you able to fold your strip that went across the center of the circle?
4. What do we call that ratio?

answers at the bottom of the page

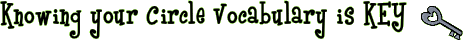The key in finding circumference is knowing the vocabulary. Yep, that's right, and having done the activity dealing with π won't hurt either. Why? Because the answer is right there! To get the circumference of a circle, you simply do the math.

You might be thinking, "Huh?" right about now. Let's see what we're talking about.

Example #1: Strictly Mathematical

So, if we want the Circumference in this equation, mathematically, we need to get the diameter out from the denominator, right?

How do we do that? Multiply both sides of the equation by the diameter.

The two diameters are cancelled out on the right.

What are we left with?

OMG! The answer!

Example #2: Estimation

You can ALWAYS estimate the circumference! Remember the finding π activity and how the diameter strip folded three times and a little bit to go around the can? Well, then this will give you the perfect way to estimate the circumference of any circle. Check it out.

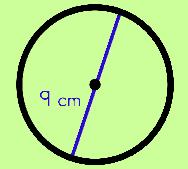
Say you have a circle and you know the diameter. In this case, the diameter is 9 cm.

1. Multiply the diameter by 3 (d • 3) = 9 • 3 = 27
2. This gives you an estimate of the circumference.

So, for this circle, the approximate circumference is 27 cm.

Example #3: Circumference Formula

Let's use the same circle from Example #2 but this time, we will go for the 'real' circumference measurement using the actual formula. We can check it against our estimation to see how close we were.

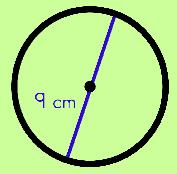
We know the diameter measurement is 9 cm. This time, instead of using an approximate measure, we will use the formula from the mathematical example (Example #1). Instead of multiplying by three, we will multiply by π.

Multiply the diameter by π (d • π) = 9 • π ≈ 9 • 3.1415 ≈ 28.2735

The approximate circumference is 28.2735 cm if we use π ≈ 3.1415 or we can leave our answer in π then our circumference would be 9π.

Did we come close to our estimate?

Our estimate was 27 and approximate answer was 28.2735–

Yep, pretty close since when we multiplied we used a number a bit LARGER than 3 so we would expect to get a little bit larger number than our estimate! YAY!

QUESTION: What if you know the radius, not the diameter?

What would happen if you know the radius of a circle instead of the diameter? Again, vocabulary is key!

Think to yourself, "What is the relationship between the radius and the diameter of a circle?"

A diameter is made up of two radii so you can use the same formula; just substitute 2r for the d!

Let's try a problem, shall we?

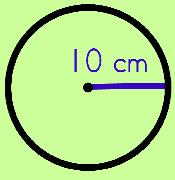
We know the radius measurement is 10 cm. We know that it takes TWO radii to make one diameter (2r = d), so…

1. Multiply the radius by 2 (2 • r) = 2 • 10 = 20. This gives us the diameter.
2. Now, we can finish up! πd = C so, π • 20 = 20π OR 20 • 3.1415 ≈ 62.83

The approximate circumference is 62.83 cm if we use π ≈ 3.1415 or we can leave our answer in π then our circumference would be 20π. (If we were to estimate the circumference, it would be 3 • 20 = 60)

Download a practice page. Circumference practice

Answers to Mini Quiz

1. What do we call the distance across a circle, through the center? diameter
2. What do we call the distance around a circle? Circumference
3. Approximately how many times were you able to fold your strip that went across the center of the circle? three times with a little leftover
4. What do we call that ratio? Pi