Finding the area of a circle isn't the easiest thing because a circle is, well, round. But, if you are familiar with finding the area of other polygons, then circles will not be very difficult. Promise!

Start by gathering up the following materials:

• circular coffee filter

• scissors

• glue or glue-stick

• sheet of paper

• pencil

• calculator

Step 1: Fold the Coffee Filter

Begin by folding the coffee filter into sectors (like the sections of an orange). First, fold it in half. The first fold is called the…(can you think of the name? hmm…the diameter!). Now, fold it in half again. Oooh, what's the name now? (hint: half of a diameter is a … radius!). Okay, fold it in half yet again.

Step 2: Cut the Sectors

Using the scissors, cut out the sectors. You will end up with lots of little things that look sort of like triangles.

Taking a look at one of the sectors, we know that the sides are the radii, right? So, we can use variables to name them, r.

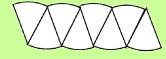
Step 3: Put the sectors together

Gather up all the sectors and on the blank sheet of paper, begin laying the sectors out in puzzle-style, alternating point up, point down, in an AB pattern until all the sectors are used up. You will end up with something that looks like this:

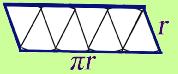
Step 4: Glue the sectors down

Glue the sectors down. Now, think for a second about what you already know about circles. Then you did some folding and cutting and re-arranging. See if you can rationalize what has now occurred.

1. You started with a coffee filter with a circumference of C = πd.
2. After folding and cutting, you had a bunch of sectors with sides of r and πr.
3. You re-arranged the sectors forming a shape that sort of resembles a parallelogram.
4. If we follow the formula for finding the area of a parallelogram, it stands to reason that finding the area of a circle would be:

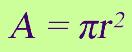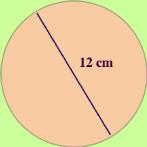
So, let's try it with some numbers, shall we? Let's say that we have the following circle.

Here is a circle with diameter of 12 cm. What is its area?

Think it through…You know what the area formula is.

What information do you have?

You know the diameter is 12 but you need to have a radius measure.

How do you find the radius? Think…ahh! A radius is half of a diameter!

Take half of 12 and you get 6.

Now, use the Substitution Property and put the 6 in for the r.