Now, both a square and a rectangle are parallelograms. What if you have one of those other parallelograms? hmm? Any thoughts? WELL, let's see how this one works out, shall we? (It's pretty cool, truly.)

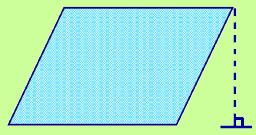
Here's a parallelogram. Just like with a rectangle, we have a base and a height, but, because we don't happen to have a perpendicular side, we have to be given the height (by dropping an altitude).

What do you predict just might be the area formula for a parallelogram?

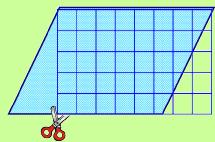
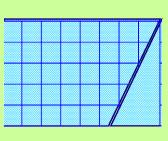
To give you a hint, let's put a piece of grid paper over the parallelogram so you can see those little squares.

Okay, now let's use some scissors to cut (as shown) the triangle that can be formed from dropping an altitude (or giving the height). Take that triangle and slide it over, along the base. What new shape have you made? Is it…could it possibly be…a rectangle? It is! Amazing!

You can now probably come up with a formula for finding the Area of a parallelogram.

And, while we're at it, let's write out the equation for our parallelogram.

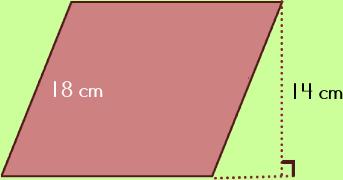
Remember to look for the right angle symbol. This will help you determine which numbers are the base and height.

Challenge: Find the area of the parallelogram below. You can do it!

Remember: Since the cm is also squared, the units will be 'square units.'