The Greatest Common Factor (GCF) is the largest number that can evenly divide two numbers. In other words, it is the greatest common divisor or factor that two numbers share. This is what you use when you reduce a fraction to lowest terms (simplify a fraction).

There are several ways that you can find the GCF (or GCD, the Greatest Common Divisor) of two numbers.

In elementary school, most of the time the method used to teach the concept is to list all of the factors of the numbers like this:

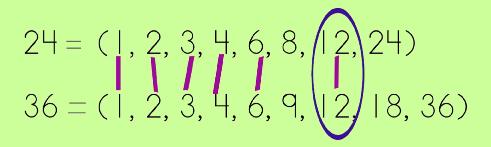Then, you'd match up those factors that both numbers share until you come to the one factor that is the largest.

The largest matching pair is the GCF.
The GCF of 24 and 36 is 12.

A much more effective method, when dealing with larger numbers (particularly when you may not know all of the factors off the top of your head!) is to use Prime Factorization. By making a factor tree to factor out all the prime numbers and then finding what factors they have in common is a not only an easier way to find the GCF but, when dealing with larger numbers, much easier in case you don't know what all the factors are!

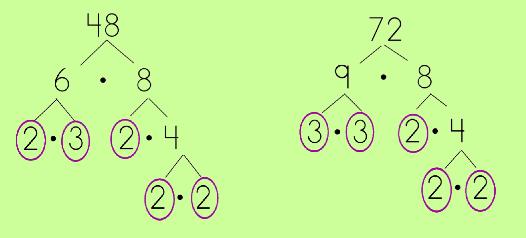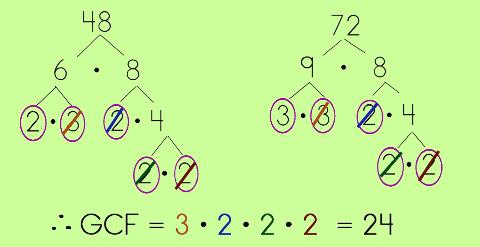
Let's try it with 48 ad 72.

Step #1: Make a factor tree for 48 and a factor tree for 72.

Prime factor the numbers, circling the primes at the end.

Step #2: Compare the prime numbers (factors) that you circled at the bottom of each factor tree.

Cross off MATCHING PAIRS (note how the matching pairs in the example are color-coded).

Step #3: Take one from each of the pairs and make a multiplication equation to get your Greatest Common Factor.

Now, there's another method, and I don't know what its' name may even be, but I think it is a GREAT way to find the Greatest Common Factor/Greatest Common Divisor for a pair of numbers. In fact, a former 6th grade student taught me this method, oh, 20+ years ago and to do this day, it is one of my faves! It can be found as the 'prime factorization division method,' but I like 6th Grader Method, myself.

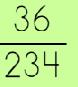This time, we are starting with a fraction and we want to reduce it to lowest terms.

(Note: it could even be just two numbers like 36 and 234)

Step #1: Re-write the fraction (or numbers) horizontally like this:

Step #2: Now, draw a NEW type of division-like bar that is a flipped version:

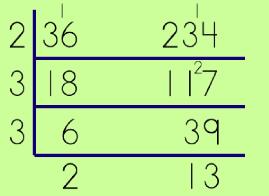
Step #3: Now, looking at both numbers see if you can find a number that is a factor of each OR, think of it as 'what number can each be divided by.'

For example, since 36 and 234 are both even numbers, they can both be divided by 2. Put the divisor on the left and the quotient under each dividend.

Continue making the division bar and finding numbers that divide the 'new' numbers.

It will be helpful if you are familiar with divisibility rules! For example, 117 is divisible by 3 because if I add 1+1+7 I get 9 and 9 is a multiple of 3. I already know that 18 is a multiple of 3…

*Did you see a different number that I could have divided by instead of 3?

If necessary, go and check your Sieve of Eratosthenes.

Step #4: Once if you have gotten down to the prime factors (you have now prime factored the two original numbers), you're almost done!

Take a look at the numbers that are along the OUTER LEFT SIDE.

Write these numbers in an equation.

GCF = 2 • 3 • 3

GCF = 18

Easy-peasy, lemon-squeezey!

FYI: In case you were wondering about the 'extra' numbers along the bottom…IF you multiplied ALL the numbers on the outer edge, you will come up with the Least Common Multiple of the two numbers.

LCM = 2 • 3 • 3 • 2 • 13

LCM = 468

For some extra practice in finding the Greatest Common Factor between a pair of numbers, then, click GCF Practice Page

If you want even MORE practice, then click More GCF Practice.

©2009–2016 Sherry Skipper Spurgeon.

All Rights Reserved.