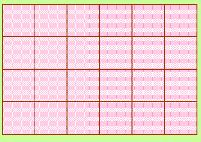
Let's check out rectangles. Now, rectangles, like squares, are parallelograms with adjacent sides meeting at perpendicular lines. These perpendicular sides provides us with a height, thus a need for some new variables.

Here's a rectangle and we'll call the shorter sides the height (measure of 4 cm) and the longer sides the base (measure of 6 cm).

Look at the rectangle. With the little square tiles, it is easy to count the area but, given the base and the height, what formula do you think you could use instead?

The capital A indicates 'Area' and the little sub-script R indicates the shape 'Rectangle.'

Did you come up with…

then, by using the Substitution Property with 6 for the b and 4 for the h come up with…

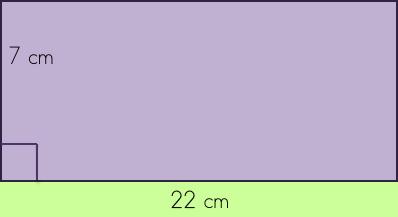
Look for the right angle symbol. This will give you the base and the height (in other words, the numbers you need to use!)

Challenge: What's the area of the rectangle below? You can do it!

Remember: Since the cm is also squared, the units will be 'square units.'

Easy-peasy, lemon-squeasy!