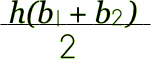If you have been working with finding the area of parallelograms, rectangles, and triangles and feel pretty comfortable with them, then when it comes to finding the area of a trapezoid, well…guess what! It will be SO easy!

Think to yourself, what other polygon name begins like trapezoid?

Hmm? Did you come up with triangle? Hooray! You're right!

And, what formula do we use for finding the area of a triangle? Do you remember? Think of your hungry tummy…food…sandwiches…*hint*hint*

Area formula for a triangle:

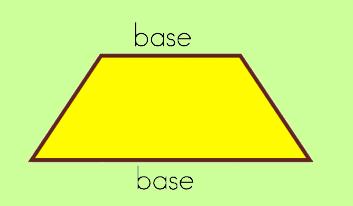
A trapezoid is a quadrilateral where one pair of opposite sides are parallel. The opposite sides that are parallel are called the bases. In the picture, you can see them easily.

Now, if you were to take the average of the bases, then, well, this is what you need for finding the area of the trapezoid!

Any idea why we need the average of the two bases? Remember how I said this is like finding the area of a triangle?

Well, if you think long and hard about it, I bet you will figure it out! If not, don't worry. The answer is coming shortly…

Mini Quiz: How would you find the average of two bases?

Add the measures of the two bases and divide by 2

IF a trapezoid's area is kind of like finding the area of a triangle, and for a triangle we need a base and a height measure…hint-hint…Get it now? Yep! That's right! Since a trapezoid has TWO bases, we need the average of the two to get a SINGLE base measure for our calculations!

SO, once you get your base 'average,' you can get to calculating your trapezoid's area. Woo-hoo! Shall we try it out?

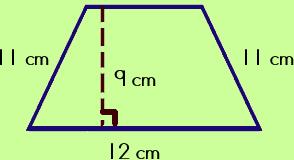
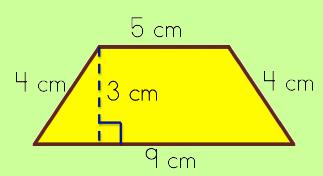
Here's a trapezoid:

Step #1: Find the bases and height of the trapezoid.

Look for the right angle symbol. This will link the two bases and the height together. The bases are 5 cm and 9 cm and the height is 3 cm.

 

NOTE: The height is ALWAYS between the two base measures.

 

Step #2: Find the average of the two bases.

So, do your calculations by finding the average of the two bases.

 

5 + 9 = 14 and 14/2 = 7 so, the average is 7 cm

 

Step #3: Multiply the height with the base average.

The height is 3 and the base average was 7 and the so multiply these two numbers.

 

3 cm • 7 cm = 21 cm² so, the area is 21 cm²

 

©2009–2016 Sherry Skipper Spurgeon.

All Rights Reserved.