|
 |
|
|
Let’s learn about prime factorization.
|
|
|
|
 |
|
|
|
|
Let's review some vocabulary.
prime number: any positive integer with EXACTLY two factors is a prime number, 1 and itself
factors: the numbers you multiply together to get the product— algebraically it would look like this
- a • b = c where a and b are the factors and c is the product
composite number: positive integers that have THREE or more whole number factors
|
|
|
|
 |
|
|
|
What if you want to find all of the factors of a number? How could you do it? EASY! Use Prime Factorization! In fact, get out your Sieve of Eratosthenes to help you. This is a great tool because it can help provide a way for you to check for prime numbers.
Prime Factorization is a method used to find all of the prime factors of a number. It utilizes a tree diagram for organizing your factors.
Let’s try it using the number 24.
|
|
|
 |
|
|
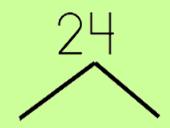
Step 1: Make a tree
- Start by writing the number and then drawing two tree branches underneath.
|
|
|
|
|
 |
|
|
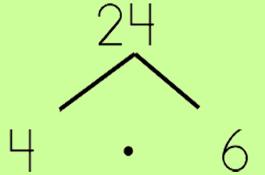
Step 2: Begin factoring…
- Think of the factors of the number (or, if this seems hard, think, "What can I divide this number evenly by?" since sometimes it is easier to think backwards). Write down the two numbers at the end of the tree branches.
-
- Keep factoring the numbers…until you get down to prime numbers.
-
-
-
-
-
-
-
-
-
-
-
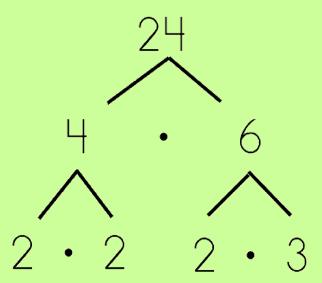
- In this next example, you will see how the numbers 4 and 6 have been factored further until we get down to the primes.
|
|
|
|
 |
|
|
|
|
 |
|
|
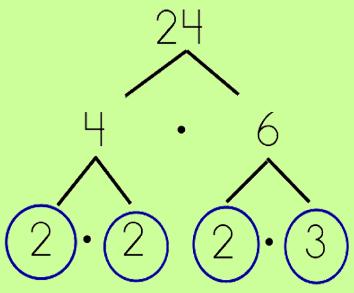
Step 3: Circle the Prime Numbers
- When you get to the prime factors, circle them.
|
|
|
|
|
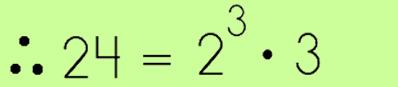 |
|
|
Step 4: Write the Prime Numbers using Exponents
- Re-write the prime numbers as an expression, using exponents. Voila!
|
|
|
|
 |
|
|
If you want even MORE practice, then click More Prime Factorization Practice.
|
|
|